Which Describes the Combined Variation in the Formula

A π r2. H varies directly with A and inve.

Joint Or Combined Variation Video Lessons Examples And Solutions

V varies directly with h.

. One of the group. In the language of variation this equation means. B and h vary inversely.

If z increases y decreases. Example 1 If y varies. For example if z varies directly as x and inversely as y we have the following combined variation equation.

Vlengthwidthheight Vlwh here we see that volume is directly proportional to width length and height. Combined variation mixes both direct and inverse variation. Describe the combined variation that is modeled by each formula.

Set up 2 variation equations the first using k_ 1 and the second k_ 2 as constants. V varies directly with a h and r2. Numbers are mixed matched computed jumbled and ultimately combined.

H varies inversely with A and b. Perhaps the most important historical discovery of this type of combined variation is Newtons law of universal gravitation which states that the gravitation force of attraction F between two particles is jointly proportional to their masses m and M and inversely proportional to the square of the distance d between them. So this equation is modeling.

Here y varies directly with x and y varies inversely with z. A 50-kg object moving at a velocity of 20 meters per second has 10000 joules of kinetic energy. Y k x z.

H varies jointly with 2 and A and inversely with b. V f rh Πr²h where V is the volume and is a function of radius and height. A V varies jointly as lw and h.

To find k use the given condition. So weve studied direct and ah inverse variation before and now we have some combination of the two and we need to explain how it works in this equation. Which answer is an example of an experimental study.

D f rt rt where d is. Correct answer to the question Which describes the combined variation in the formula V xr2h. When we have a variation where one quantity varies as the product of two or more other quantities we have what is called joint variation.

If y is inversely proportional to x and k is a constant the equation is of the form. Sector area is a fraction of a circles _________________. Describe the combined variation that is modeled by each formula.

Combined variation is a variation where a quantity depends on two or more other quantities and varies directly with some of them and varies inversely with others. Vlwh-----Ive never hear of combined variation but here goes. P f lw 2l 2w where P is the perimeter and is a function of width and length.

V Bh 3. To convert to an equation multiply by k the constant. A researcher asks two groups of students to solve a difficult math problem.

HfracVpi r2. When one goes up in value the other goes down. T kd2 3x k T d2 3x 18 9 2 1.

V varies jointly with h and 2. H varies jointly with A and b. V varies inversely with h and 12.

You can put this solution on YOUR website. Our job is to explain that combined variation present in this formula. Which describes the combined variation in the formula h2ab.

Its a double dose of variation. Up to 10 cash back Combined variation describes a situation where a variable depends on two or more other variables and varies directly with some of them and varies inversely with others when the rest of the variables are held constant. V varies directly with B.

S is told that members will receive a. Joint variation is a variation where a quantity varies directly as the product of two or more other quantities. And the constant of variation is k π.

If x decreases y decreases. The kinetic energy K of an object varies jointly with the mass of the object and the square of the velocity of the object. V and l or V and w or V and h are all directly related.

V varies directly with r2. The first equation is inverse variation and the second equation is direct variation. Suppose y varies jointly as x and z.

Which describes the combined variation in the formula V πr2h. Y kxz y varies jointly as x and z when there is some nonzero constant k. T kd2 3x.

Therefore the correct answer is. How many joules of kinetic energy does a 25-kg object moving at a velocity of 10 meters per second have. T 18 when x 8 and d 3.

Joint Variation or Combined Variation is when one quantity varies directly as the product of at least two other quantities. When one variable increases the other decreases in proportion so that the product is unchanged. Describe the combined variation that is modeled by each formula.

When one goes up the other goes up-----l and w or l and h or w and h are all indirectly related. This is the concept of proportionality. If x increases y increases.

V varies directly with h. In respect to this how do you solve combined variations step by step. What is Joint Variation or Combined Variation.

Answer by stanbon 75887 Show Source. In other words F is related to m. The area A varies directly with the square of the radius r.

Which describes the combined variation in the formula h2Ab Get the answers you need now. V varies inversely with a h and r2. Solve for k_ 1 and k_ 2 separately using the fact that y and z are both 12 when x3.

This formula is an example of direct variationDirect variation means that in the. We are required to find the combined variation for the volume formula given by. The function notation of the formulas can be written as.

Z k x y. Equation is 2 2 T d2 3x 2 2. R2 and h vary inversely.

New questions in Mathematics. The general form looks like this. Y k x.

Joint and Combined Variation.

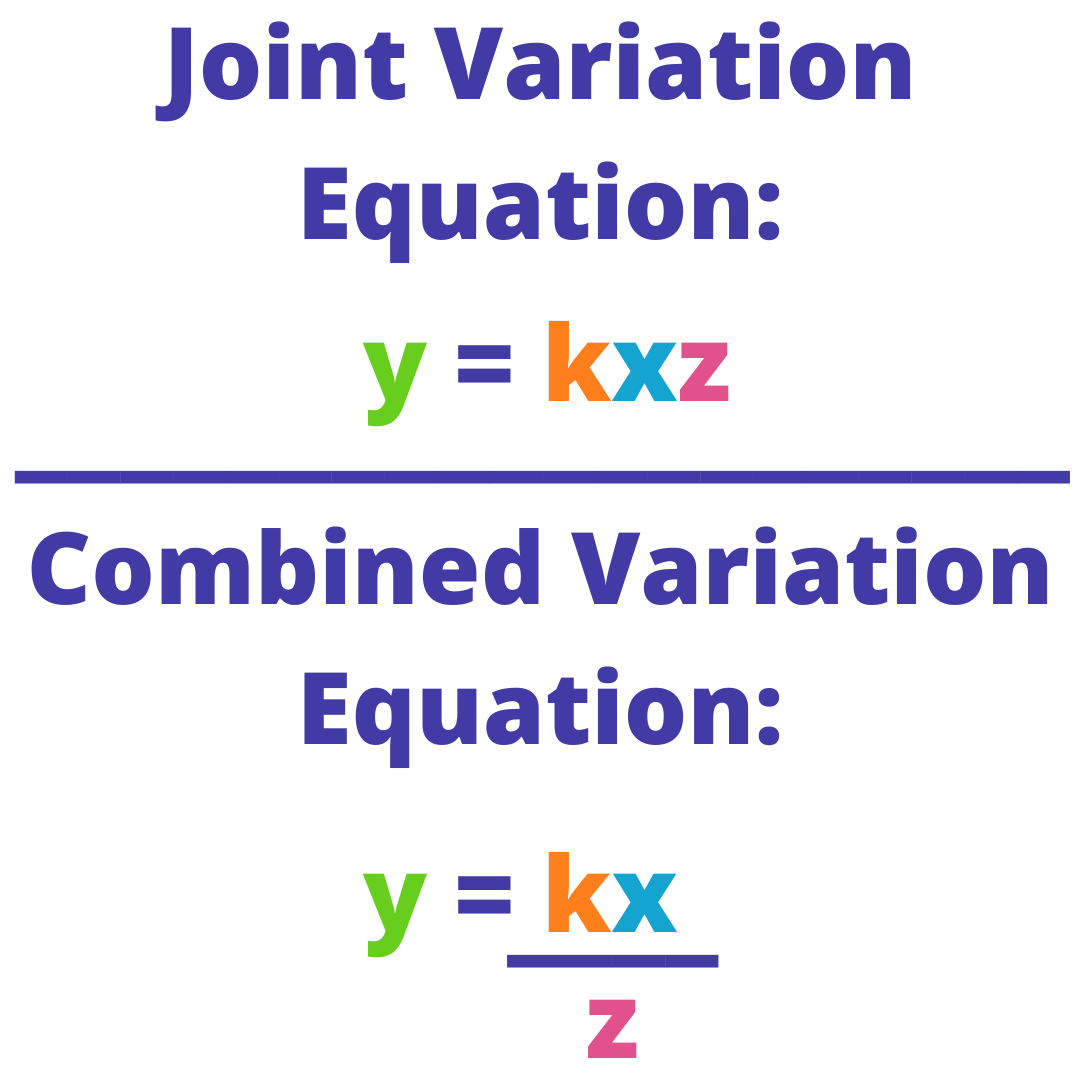
Joint Variation And Combined Variation Definitions Expii

Joint Variation And Combined Variation Definitions Expii

Solved 6 V Which Describes The Combined Variation In The Chegg Com

Which Describes The Combined Variation In The Formula H V Pie R2 Brainly Com

Share this post